Giải bài 48 49 50 51 52 trang 29 30 sgk Toán 9 tập 1

Hướng dẫn giải Bài §7. Biến đổi đơn giản biểu thức chứa căn thức bậc hai (tiếp theo), chương I - Căn bậc hai. Căn bậc ba, sách giáo khoa toán 9 tập một. Nội dung bài giải bài 48 49 50 51 52 trang 29 30 sgk toán 9 tập 1 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần đại số có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 9.

Lý thuyết

1. Khử mẫu của biểu thức lấy căn

Khi biến đổi biểu thức chứa căn bậc hai, người ta có thể sử dụng phép khử mẫu của biểu thức lấy căn.

Một cách tổng quát: Với các biểu thức A, B mà (A.Bgeq 0 và Bneq 0, ta có sqrt{frac{A}{B}}=frac{sqrt{AB}}{|B|})

2. Trục căn thức ở mẫu

Một cách tổng quát:

Với các biểu thức A, B mà (B>0), ta có: (frac{A}{sqrt{B}}=frac{Asqrt{B}}{B})

Với các biểu thức A, B, C mà (Ageq 0 và Aneq B^2), ta có (frac{C}{sqrt{A}pm B}=frac{C(sqrt{A}pm B)}{A-B^2})

Với các biểu thức A, B, C mà (Ageq 0, Bgeq 0 và Aneq B), ta có (frac{C}{sqrt{A}pm sqrt{B}}=frac{C(sqrt{A}pm sqrt{B})}{A-B})

Dưới đây là phần Hướng dẫn trả lời các câu hỏi có trong bài học cho các bạn tham khảo. Các bạn hãy đọc kỹ câu hỏi trước khi trả lời nhé!

Câu hỏi

1. Trả lời câu hỏi 1 trang 28 sgk Toán 9 tập 1

Khử mẫu của biểu thức lấy căn

a) (displaystyle sqrt {{4 over 5}} )

b) (displaystyle sqrt {{3 over {125}}} )

c) (displaystyle sqrt {{3 over {2{a^3}}}} ) với a > 0

Trả lời:

Ta có:

a) (displaystyle sqrt {{4 over 5}} = sqrt {{{4.5} over {5.5}}} = {{sqrt {4.5} } over {sqrt {{5^2}} }} = {{2sqrt 5 } over 5})

b) (displaystyle sqrt {{3 over {125}}} = sqrt {{{3.125} over {125.125}}} = {{sqrt {3.125} } over {sqrt {{{125}^2}} }} = {{5sqrt {15} } over {125}} = {{sqrt {15} } over {25}})

c) (sqrt {dfrac{3}{{2{a^3}}}} = dfrac{{sqrt 3 }}{{sqrt {2{a^3}} }} = dfrac{{sqrt 3 }}{{sqrt {{a^2}.2a} }} = dfrac{{sqrt 3 }}{{left| a right|sqrt {2a} }} = dfrac{{sqrt 3 }}{{asqrt {2a} }}) ( = dfrac{{sqrt 3 .sqrt {2a} }}{{asqrt {2a} .sqrt {2a} }} = dfrac{{sqrt {6a} }}{{2{a^2}}})

2. Trả lời câu hỏi 2 trang 29 sgk Toán 9 tập 1

Trục căn thức ở mẫu:

a) (displaystyle {5 over {3sqrt 8 }};,,{2 over {sqrt b }}) với b > 0

b) (displaystyle {5 over {5 - 2sqrt 3 }};,,,{{2a} over {1 - sqrt a }}) với (a ge 0) và (a ne 1)

c) (displaystyle {4 over {sqrt 7 + sqrt 5 }};,,,{{6a} over {2sqrt a - sqrt b }}) với a > b > 0

Trả lời:

Ta có:

a) +) (displaystyle {5 over {3sqrt 8 }} = {{5sqrt 8 } over {3sqrt 8 .sqrt 8 }} = {{5sqrt 8 } over {3.8}} = {5 over {24}}sqrt 8 )

+) (displaystyle {2 over {sqrt b }} = {{2sqrt b } over {sqrt b .sqrt b }} = {2 over b}sqrt b )

b) (displaystyle {5 over {5 - 2sqrt 3 }} = {{5left( {5 + 2sqrt 3 } right)} over {left( {5 - 2sqrt 3 } right)left( {5 + 2sqrt 3 } right)}} displaystyle = {{5left( {5 + 2sqrt 3 } right)} over {25 - 12}} = {{5left( {5 + 2sqrt 3 } right)} over {13}})

(displaystyle {{2a} over {1 - sqrt a }} = {{2aleft( {1 + sqrt a } right)} over {left( {1 - sqrt a } right)left( {1 + sqrt a } right)}} displaystyle = {{2aleft( {1 + sqrt a } right)} over {1 - a}})

c) (displaystyle {4 over {sqrt 7 + sqrt 5 }} = {{4left( {sqrt 7 - sqrt 5 } right)} over {left( {sqrt 7 + sqrt 5 } right)left( {sqrt 7 - sqrt 5 } right)}} displaystyle = {{4left( {sqrt 7 - sqrt 5 } right)} over {7 - 5}} = 2left( {sqrt 7 - sqrt 5 } right))

(displaystyle {{6a} over {2sqrt a - sqrt b }} = {{6aleft( {2sqrt a + sqrt b } right)} over {left( {2sqrt a - sqrt b } right)left( {2sqrt a + sqrt b } right)}} displaystyle = {{6aleft( {2sqrt a + sqrt b } right)} over {4a - b}})

Dưới đây là Hướng dẫn giải bài 48 49 50 51 52 trang 29 30 sgk toán 9 tập 1. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần đại số 9 kèm bài giải chi tiết bài 48 49 50 51 52 trang 29 30 sgk toán 9 tập 1 của bài §7. Biến đổi đơn giản biểu thức chứa căn thức bậc hai (tiếp theo) trong chương I - Căn bậc hai. Căn bậc ba cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

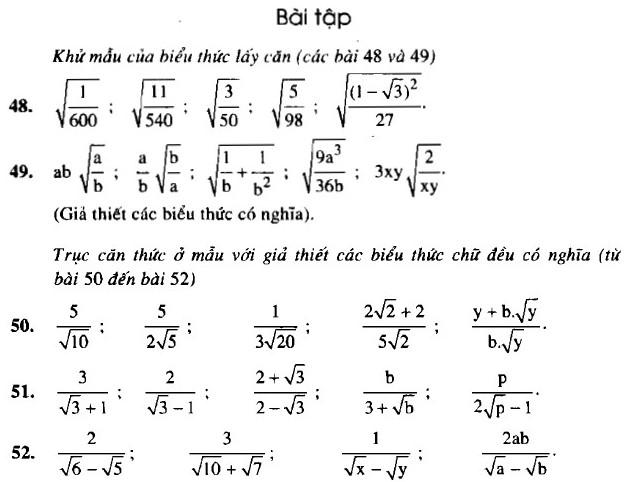
1. Giải bài 48 trang 29 sgk Toán 9 tập 1

Khử mẫu của biểu thức lấy căn:

$sqrt{frac{1}{600}};sqrt{frac{11}{540}};sqrt{frac{3}{50}};$

$sqrt{frac{5}{98}}; sqrt{frac{(1-sqrt{3})^{2}}{27}}$.

Bài giải:

Ta có:

♦ (sqrt{dfrac{1}{600}}=dfrac{sqrt 1}{sqrt{600}})

(=dfrac{ 1}{sqrt{6.100}})(=dfrac{1}{sqrt{6.10^2}})

(=dfrac{ 1}{sqrt{6}.sqrt{10^2}})(=dfrac{ 1}{10sqrt{6}})

(=dfrac{ 1.sqrt 6}{10.6})(=dfrac{ sqrt 6}{60})

♦ $sqrt{dfrac{11}{540}}=dfrac{sqrt{11}}{sqrt{540}}$

$=dfrac{sqrt{11}}{sqrt{36.15}}=dfrac{sqrt{11}}{sqrt{36}.sqrt{15}}$

$=dfrac{sqrt{11}}{sqrt{6^2}.sqrt{15}}=dfrac{sqrt{11}}{6sqrt{15}}$

$=dfrac{sqrt{11}.sqrt{15}}{6.15}=dfrac{sqrt{11.15}}{90}=dfrac{sqrt{165}}{90}$.

♦ $sqrt{dfrac{3}{50}}=dfrac{sqrt 3}{sqrt{50}}$

$=dfrac{sqrt 3}{sqrt{25.2}}=dfrac{sqrt{3}}{sqrt{25}.sqrt{2}}$

$=dfrac{sqrt{3}}{sqrt{5^2}.sqrt{2}}=dfrac{sqrt{3}}{5sqrt{2}}$

$=dfrac{sqrt{3}.sqrt 2}{5.2}=dfrac{sqrt{3.2}}{10}=dfrac{sqrt{6}}{10}$

♦ $sqrt{dfrac{5}{98}}=dfrac{sqrt 5}{sqrt {98}}$

$=dfrac{sqrt 5}{sqrt{49.2}}=dfrac{sqrt 5}{sqrt{49}sqrt{2}}$

$=dfrac{sqrt 5}{sqrt{7^2}.sqrt 2}=dfrac{sqrt 5}{7sqrt 2}$

$=dfrac{sqrt 5 . sqrt 2}{7. 2}=dfrac{sqrt {5. 2}}{14}=dfrac{sqrt{10}}{14}$.

♦ $sqrt{dfrac{(1-sqrt{3})^{2}}{27}}=dfrac{sqrt{(1-sqrt 3)^2}}{sqrt {27}}$

$=dfrac{sqrt{(1-sqrt 3)^2}}{sqrt {9.3}}=dfrac{sqrt{(1-sqrt 3)^2}}{sqrt {3^2.3}}$

$=dfrac{|1-sqrt{3}|}{3sqrt {3}}$

Vì (1< 3 Leftrightarrow sqrt 1 < sqrt 3 Leftrightarrow 1< sqrt 3) ( Leftrightarrow 1- sqrt 3 < 0)

(Leftrightarrow |1- sqrt 3|=-(1-sqrt 3)=-1 + sqrt 3 = sqrt 3 -1.)

Do đó:

$dfrac{|1-sqrt{3}|}{3sqrt {3}}=dfrac{sqrt{3}-1}{3sqrt {3}}$

$=dfrac{sqrt 3(sqrt{3}-1)}{9}=dfrac{3-sqrt 3}{9}.$

2. Giải bài 49 trang 29 sgk Toán 9 tập 1

Khử mẫu của biểu thức lấy căn

$absqrt{frac{a}{b}}; frac{a}{b}sqrt{frac{b}{a}}; sqrt{frac{1}{b}+frac{1}{b^{2}}};$

$ sqrt{frac{9a^{3}}{36b}}; 3xysqrt{frac{2}{xy}}.$

(Giả thiết các biểu thức có nghĩa)

Bài giải:

Theo đề bài các biểu thức đều có nghĩa. Do đó ta có:

$absqrt{dfrac{a}{b}}=absqrt{dfrac{a.b}{b.b}}=absqrt{dfrac{ab}{b^2}}$

$=abdfrac{sqrt{ab}}{sqrt{b^2}}=abdfrac{sqrt{ab}}{left | b right |}.$

Nếu ( b ge 0) thì (|b|=b Rightarrow abdfrac{sqrt{ab}}{left | b right |}=abdfrac{sqrt{ab}}{b}=asqrt{ab}).

Nếu ( b < 0) thì (|b|=-b Rightarrow abdfrac{sqrt{ab}}{left | b right |}=-abdfrac{sqrt{ab}}{b}=-asqrt{ab}).

( dfrac{a}{b}sqrt{dfrac{b}{a}}=dfrac{a}{b}sqrt{dfrac{b.a}{a.a}}=dfrac{a}{b}sqrt{dfrac{ab}{a^2}})

(=dfrac{a}{b}.dfrac{sqrt{ab}}{sqrt{a^2}})(=dfrac{a}{b}.dfrac{sqrt{ab}}{|a|})(=dfrac{asqrt{ab}}{b|a|})

Nếu (ageq 0) thì ( |a|=a Rightarrow dfrac{asqrt{ab}}{b|a|}=dfrac{asqrt{ab}}{ab}=dfrac{sqrt{ab}}{b} .)

Nếu (a<0) thì (|a|=-a Rightarrow dfrac{asqrt{ab}}{b|a|}=-dfrac{asqrt{ab}}{ab}=-dfrac{sqrt{ab}}{b} .)

(sqrt{dfrac{1}{b}+dfrac{1}{b^2}}=sqrt{dfrac{b}{b^2}+dfrac{1}{b^2}}=sqrt{dfrac{b+1}{b^2}})

(=dfrac{sqrt{b+1}}{sqrt{b^2}}=dfrac{sqrt{b+1}}{|b|}).

Nếu (b ge 0) thì (|b|=b Rightarrow dfrac{sqrt{b+1}}{|b|}=dfrac{sqrt{b+1}}{b}).

Nếu (-1 le b < 0) thì (|b|=-b Rightarrow dfrac{sqrt{b+1}}{|b|}=-dfrac{sqrt{b+1}}{b}).

(sqrt{dfrac{9a^3}{36b}}=sqrt{dfrac{9}{36}}.sqrt{dfrac{a^3}{b}}=sqrt{dfrac{1}{4}}.sqrt{dfrac{a^3.b}{b.b}})

(=dfrac{1}{2}.sqrt{dfrac{a^2.ab}{b^2}})(=dfrac{1}{2}.dfrac{sqrt{a^2}.sqrt{ab}}{sqrt{b^2}})

(=dfrac{1}{2}.dfrac{|a|sqrt{ab}}{|b|}=dfrac{|a|sqrt{ab}}{2|b|}).

Nếu (a ge 0, b ge 0) thì (|a|=a, |b| =b Rightarrow dfrac{|a|sqrt{ab}}{2|b|}=dfrac{asqrt{ab}}{2b}).

Nếu (a < 0, b < 0) thì (|a|=-a, |b| =-b Rightarrow dfrac{|a|sqrt{ab}}{2|b|}=dfrac{asqrt{ab}}{2b}).

Theo đề bài (sqrt{dfrac{9a^3}{36b}}) có nghĩa nên (a, b) cùng dấu, do đó chỉ cần xét 2 trường hợp (a, b) cùng âm hoặc cùng dương.

(3xysqrt{dfrac{2}{xy}}=3xy.sqrt{dfrac{2.xy}{xy.xy}}=3xy.dfrac{sqrt{2xy}}{sqrt{(xy)^2}})

(=3xy.dfrac{sqrt{2xy}}{|xy|}) (=dfrac{3xy.sqrt{2xy}}{xy}=3sqrt{2xy}).

Vì theo đề bài (sqrt{dfrac{2}{xy}}) có nghĩa nên (dfrac{2}{xy} ge 0 Leftrightarrow xy ge 0 Rightarrow |xy|=xy).

3. Giải bài 50 trang 30 sgk Toán 9 tập 1

Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa:

$frac{5}{sqrt{10}}; frac{5}{2sqrt{5}}; frac{1}{3sqrt{20}}; $

$frac{2sqrt{2}+2}{5sqrt{2}}; frac{y+bsqrt{y}}{b.sqrt{y}}$

Bài giải:

+ Ta có:

$dfrac{5}{sqrt{10}}=dfrac{5.sqrt{10}}{sqrt{10}.sqrt{10}}$

$=dfrac{5sqrt{10}}{(sqrt{10})^2}=dfrac{5sqrt{10}}{10}$

$=dfrac{5.sqrt{10}}{5.2}=dfrac{sqrt{10}}{2}$.

+ Ta có:

$dfrac{5}{2sqrt{5}}=dfrac{5.sqrt 5}{2sqrt 5.sqrt 5}$

$=dfrac{5sqrt{5}}{2.(sqrt 5.sqrt 5)}=dfrac{5sqrt{5}}{2(sqrt 5)^2}$

(=dfrac{5sqrt 5}{2.5}=dfrac{sqrt 5}{2}).

+ Ta có:

$dfrac{1}{3sqrt{20}}=dfrac{1.sqrt{20}}{3sqrt{20}.sqrt{20}}$

$=dfrac{sqrt{20}}{3.(sqrt{20}.sqrt{20})}=dfrac{sqrt{20}}{3.(sqrt{20})^2}$

$=dfrac{sqrt{20}}{3.20}=dfrac{sqrt{2^2.5}}{60}$

$=dfrac{2sqrt 5}{60}=dfrac{2sqrt 5}{2.30}=dfrac{sqrt 5}{30}$.

+ Ta có:

$dfrac{(2sqrt{2}+2)}{5.sqrt 2}=dfrac{(2sqrt 2+2).sqrt 2}{5sqrt 2. sqrt 2}$

$=dfrac{2sqrt 2.sqrt 2+2.sqrt 2}{5.(sqrt 2)^2}=dfrac{2.2+2sqrt 2}{5.2}$

$=dfrac{2(2+sqrt 2)}{5.2}=dfrac{2+sqrt 2}{5}$.

+ Ta có:

$dfrac{y+bsqrt{y}}{bsqrt{y}}=dfrac{(y+bsqrt y).sqrt y}{bsqrt y .sqrt y}$

$=dfrac{ysqrt y+bsqrt y.sqrt y}{b.(sqrt y)^2}= dfrac{ysqrt y+b(sqrt y)^2}{by}$

$=dfrac{ysqrt y+by}{by}=dfrac{y(sqrt y+b)}{b.y}=dfrac{sqrt y+b}{b}$.

4. Giải bài 51 trang 30 sgk Toán 9 tập 1

Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa:

$frac{3}{sqrt{3}+1};frac{2}{sqrt{3}-1};frac{2+sqrt{3}}{2-sqrt{3}};$

$frac{b}{3+sqrt{b}};frac{p}{2sqrt{p}-1}$

Bài giải:

Ta có:

$frac{3}{sqrt{3}+1}=frac{3(sqrt{3}-1)}{(sqrt{3}-1)(sqrt{3}+1)}$

$=frac{3sqrt{3}-3}{2}$

$frac{2}{sqrt{3}-1}=frac{2(sqrt{3}+1)}{(sqrt{3}+1)(sqrt{3}-1)}$

$=frac{2(sqrt{3}+1)}{2}=sqrt{3}+1$

$frac{2+sqrt{3}}{2-sqrt{3}}=frac{(2+sqrt{3})^2}{(2+sqrt{3})(2-sqrt{3})}$

$=7+4sqrt{3}$

$frac{b}{3+sqrt{b}}=frac{b(3-sqrt{b})}{(3-sqrt{b})(3+sqrt{b})}$

$=frac{b(3-sqrt{b})}{9-b};(bneq 9)$

$frac{p}{2sqrt{p}-1}=frac{p(2sqrt{p}+1)}{(2sqrt{p}+1)(2sqrt{p}-1)}$

$=frac{p(2sqrt{p}+1)}{4p-1}$

5. Giải bài 52 trang 30 sgk Toán 9 tập 1

Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa:

(frac{2}{sqrt{6}-sqrt{5}};frac{3}{sqrt{10}+sqrt{7}};frac{1}{sqrt{x}-sqrt{y}};frac{2ab}{sqrt{a}-sqrt{b}})

Bài giải:

Ta có:

$frac{2}{sqrt{6}-sqrt{5}}=frac{2(sqrt{6}+sqrt{5})}{(sqrt{6}-sqrt{5})(sqrt{6}+sqrt{5})}$

$=2(sqrt{6}+sqrt{5})$

$frac{3}{sqrt{10}+sqrt{7}}=frac{3(sqrt{10}-sqrt{7})}{(sqrt{10}-sqrt{7})(sqrt{10}+sqrt{7})}$

$=sqrt{10}-sqrt{7}$

$frac{1}{sqrt{x}-sqrt{y}}=frac{(sqrt{x}+sqrt{y})}{(sqrt{x}+sqrt{y})(sqrt{x}-sqrt{y})}$

$=frac{sqrt{x}+sqrt{y}}{x-y}$

$frac{2ab}{sqrt{a}-sqrt{b}}=frac{2ab(sqrt{a}+sqrt{b})}{(sqrt{a}+sqrt{b})(sqrt{a}-sqrt{b})}$

$=frac{2ab(sqrt{a}+sqrt{b})}{a-b}$

Bài trước:

• Giải bài 43 44 45 46 47 trang 27 sgk Toán 9 tập 1

Bài tiếp theo:

• Luyện tập: Giải bài 53 54 55 56 57 trang 30 sgk Toán 9 tập 1

Xem thêm:

• Các bài toán 9 khác
• Để học tốt môn Vật lí lớp 9
• Để học tốt môn Sinh học lớp 9
• Để học tốt môn Ngữ văn lớp 9
• Để học tốt môn Lịch sử lớp 9
• Để học tốt môn Địa lí lớp 9
• Để học tốt môn Tiếng Anh lớp 9
• Để học tốt môn Tiếng Anh lớp 9 thí điểm
• Để học tốt môn Tin học lớp 9
• Để học tốt môn GDCD lớp 9

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 9 với giải bài 48 49 50 51 52 trang 29 30 sgk toán 9 tập 1!

“Bài tập nào khó đã có giaibaisgk.com“