Bộ 22 đề thi giữa kì 2 Toán 7 năm 2024 có đáp án và ma trận

Bộ đề thi giữa học kì 2 môn Toán lớp 7 sách mới năm học 2023 - 2024 là tài liệu ôn tập hữu ích dành cho các em học sinh. Tài liệu tổng hợp đề thi giữa kì 2 Toán 7 sách Chân trời sáng tạo, Kết nối tri thức, Cánh diều, giúp các em làm quen với nhiều dạng đề thi khác nhau, nâng cao kỹ năng giải đề thi. Mời các em cùng tham khảo nội dung chi tiết dưới đây.

Lưu ý: Toàn bộ 22 đề thi và đáp án có trong file tải về, mời các bạn tải về tham khảo trọn bộ.

Hoặc tải từng bộ đề theo Link sau:

1. Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo

Đề thi giữa kì 2 Toán 7 CTST - Đề 1

Ma trận đề thi giữa kì 2 Toán 7

STT

Nội dung kiến thức

Đơn vị kiến thức

Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá

Tổng

% điểm

Nhận biết

Thông hiểu

Vận dụng

Vận dụng cao

TN

TL

TN

TL

TN

TL

TN

TL

1

Tỉ lệ thức và đại lượng tỉ lệ

Tỉ lệ thức. Tính chất dãy tỉ số bằng nhau

1

5

1

57,5%

Đại lượng tỉ lệ thuận. Đại lượng tỉ lệ nghịch

2

1

2

Tam giác

Góc và cạnh của một tam giác

1

42,5%

Tam giác bằng nhau

1

2

1

Tam giác cân

1

Đường vuông góc và đường xiên

1

Đường trung trực của một đoạn thẳng

1

Tổng: Số câu

Điểm

6

(1,5đ)

2

(0,5đ)

6

(5,0đ)

2

(2,5đ)

1

(0,5đ)

17

10

Tỉ lệ

15%

55%

25%

5%

100%

Tỉ lệ chung

70%

30%

100%

Đề kiểm tra giữa kì 2 Toán 7 CTST

I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây.

Câu 1. Tỉ Lệ thức nào sau đây không được lập từ tỉ lệ thức (frac{4}{9}=frac{24}{54})?

(A. frac{4}{24}=frac{9}{54})(B. frac{54}{24}=frac{9}{4};)(C. frac{4}{54}=frac{9}{24};)

D. frac{24}{4}=frac{54}{9}.(D. frac{24}{4}=frac{54}{9}.)

Câu 2. Cho đại lượng P tỉ lệ thuận với đại lượng m theo hệ số tỉ lệ g=9,8. Công thức tính P theo m là

(A. P=frac{m}{9,8};)B. P m=9,8;C. m=9,8 P;D. P=9,8 m.

Câu 3. Cho biết x và y là hai đại lượng tỉ lệ nghịch. Khi x=6 thì y=9. Giá trị của x khi y=3 là

(A. x=frac{9}{2};)B. x=2;C. x=18;D. x=12.

Câu 4. Bộ ba độ dài đoạn thẳng nào sau đây không tạo thành một tam giác?

A. 2 cm, 3 cm, 5 cm;B. 2 cm, 4 cm, 5 cm;C. 3 cm, 4 cm, 6 cm;D. 3 cm; 4 cm; 5 cm.

Câu 5. Cho hai tam giác A B C và D E F có A B=D E ; 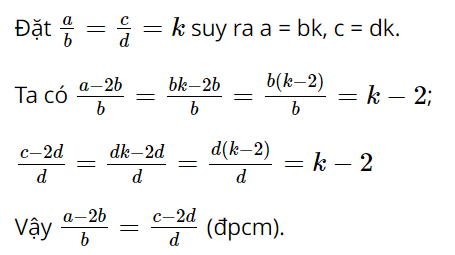widehat{A B C}=widehat{D E F} ; B C=E F.(widehat{A B C}=widehat{D E F} ; B C=E F.)

Trong khẳng định sau, khẳng định nào là sai?

A. triangle A B C=triangle D E F;(A. triangle A B C=triangle D E F;)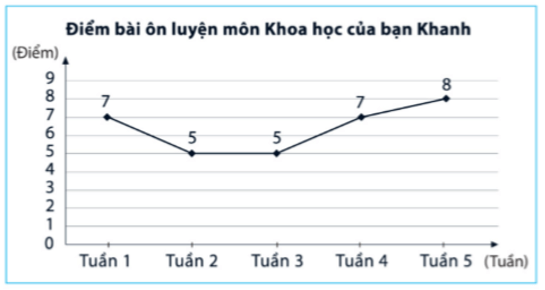B. triangle A C B=triangle D F E;(B. triangle A C B=triangle D F E;)(C. triangle A B C=triangle D F E;)(D. triangle B A C=triangle E D F.)

Câu 6. Cho 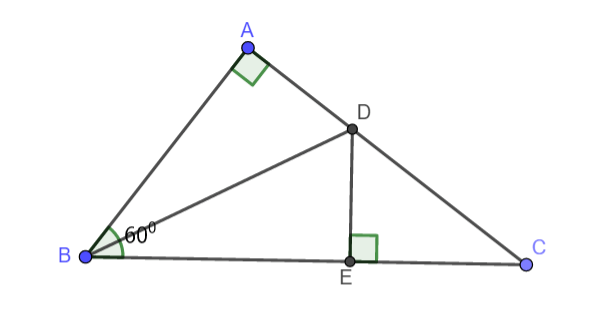Delta K L M(Delta K L M) cân tại K có (widehat{K}=116^{circ}). Số đo của (widehat{M}) là

A. 580B. 320C. 1160D. 340

Câu 7. Cho ba điểm A, B, C thẳng hàng, điểm B nằm giữa hai điểm A và C. Trên đường thẳng vuông góc với AC tại B ta lấy điểm M (điểm M không trùng với điểm B). Khi đó, khẳng định nào sau đây là đúng?

A. A M<B M;B. A M>B M;C. C M<B C;D. B M>C M.

Câu 8. Điền vào chỗ chấm: Đường trung trực của một đoạn thẳng là đường thẳng …….. với một đoạn thẳng tại trung điểm của đoạn thẳng đó.

A. song song;B. bằng;C. cắt nhau;D. vuông góc.

II. PHẦN TỰ LUẬN (8,0 điểm)

Bài 1. (1,5 điểm) Tìm số hữu tỉ x trong các tỉ lệ thức sau:

(a) frac{x}{6}=frac{-24}{18};)

(b) frac{2 x+4}{5}=frac{2 x+1}{10};)

(c) frac{x+5}{8}=frac{2}{x+5}.)

Bài 2. (1,5 điểm) Tìm a, b, c biết:

a) (frac{a}{7}=frac{b}{3}=frac{c}{4}) và b+c=35;

(b) frac{a}{3}=frac{c}{5} ; 7 b=5 c và a-b+c=62.)

Bài 3. (1,5 điểm) Hưởng ứng phong trào kế hoạch nhỏ, ba lớp 7A, 7B, 7C có 130 học sinh tham gia. Mỗi học sinh lớp 7A góp 2kg, mỗi học sinh lớp 7B góp 3kg, học sinh lớp 7C góp 4 kg. Tính số học sinh tham gia phong trào của mỗi lớp đó, biết số giấy thu được của ba lớp đó bằng nhau.

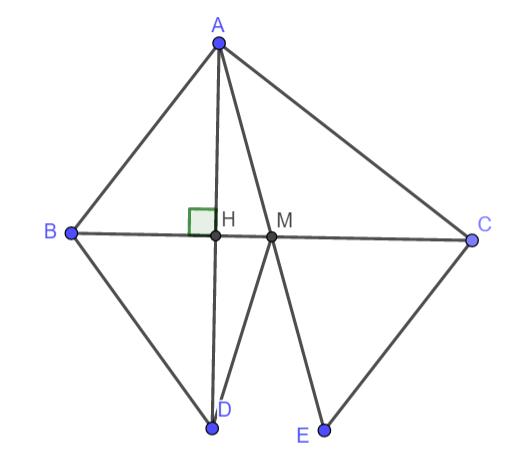
Bài 4. (3,0 điểm) Cho tam giác (triangle A B C) vuông cân tại A. Gọi M là trung điểm của cạnh BC. Lấy một điểm D bất kì thuộc cạnh BC. Qua B và C, kẻ hai đường vuông góc với cạnh AD, lần lượt cắt A D tại H và K. Gọi I là giao điểm của AM và CK.

a) Chứng minh BH=AK;

b) Chứng minh (D I perp A C;)

c) Chứng minh KM là đường phân giác của (widehat{H K C}.)

Bài 5. (0,5 điểm) Cho (a, b, c neq 0) và thỏa mãn (frac{a+b-c}{c}=frac{c+a-b}{b}=frac{b+c-a}{a}.)

Tính giá trị biểu thức (S=frac{(a+b)(b+c)(c+a)}{a b c}.)

Xem đáp án trong file tải về

Đề thi giữa kì 2 Toán 7 CTST - Đề 2

I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Thay tỉ số 1,25 : 3,45 bằng tỉ số giữa các số nguyên ta được

A. 12,5 : 34,5;

B. 29 : 65;

C. 25 : 69;

D. 1 : 3.

Câu 2. Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = -3 thì giá trị của y bằng bao nhiêu?

A. -6;

B. 0;

C. -9;

D. -1.

Câu 3. Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = -12 thì y = 8. Khi x = 3 thì y bằng

A. -32;

B. 32;

C. -2;

D. 2.

Câu 4. Cho hình vẽ sau:

Số đo x là

A. 18°;

B. 72°;

C. 36°;

D. Không xác định được.

Câu 5. Hai tam giác bằng nhau là

A. Hai tam giác có ba cặp cạnh tương ứng bằng nhau;

B. Hai tam giác có ba cặp góc tương ứng bằng nhau;

C. Hai tam giác có ba cặp cạnh, ba cặp góc tương ứng bằng nhau;

D. Hai tam giác có hai cạnh bằng nhau.

Câu 6. Một tam giác cân có góc ở đáy bằng 40° thì số đo góc ở đỉnh là

A. 50°;

B. 40°;

C. 140°;

D. 100°.

Câu 7. Cho tam giác MNP có: MN < MP, MD ⊥ NP. Khẳng định nào sau đây là đúng?

A. DN = DP;

B. MN = MP;

C. MD > MN;

D. MD < MP.

Câu 8. Điền vào chỗ trống sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.

A. Trung trực;

B. Giao điểm;

C. Trọng tâm;

D. Trung điểm.

II. PHẦN TỰ LUẬN (8,0 điểm)

Bài 1. (1,5 điểm) Tìm số hữu tỉ x trong các tỉ lệ thức sau:

c) (frac{x + 11}{14 - x} = frac{2}{3})

Bài 2. (2,0 điểm)

a. Tìm hai số a, b biết rằng 2a = 5b và 3a + 4b = 46

b. Tìm ba số a, b, c biết rằng a : b : c = 2 : 4 : 5 và a + b - c = 3

Bài 3. (1,5 điểm) Trong đợt quyên góp sách ủng hộ các bạn vùng cao, số sách mà ba lớp 7A, 7B, 7C quyên góp được tỉ lệ với ba số 5; 6; 8. Tính số sách cả ba lớp đã quyên góp, biết số sách lớp 7C quyên góp nhiều hơn số sách của lớp 7A quyên góp là 24 quyển.

Bài 4. (3,0 điểm)

Cho tam giác ABC (AB < AC) M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho AM = EM.

a. Chứng minh: ΔAMB = ΔMCE

b. Từ A kẻ AH vuông góc với BC. Trên tia đối của tia HA lấy điểm D sao cho HA = HD. Chứng minh: CE = BD

c. Tam giác AMD là tam giác gì? Vì sao?

Đáp án đề thi Toán 7 giữa kì 2 CTST

I. Trắc nghiệm

1. C

2. A

3. A

4.B

5. C

6. D

7. D

8. D

II. PHẦN TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm)

c. (frac{x + 11}{14 - x} = frac{2}{3})

3(x + 11) = 2(14 - x)

3x + 33 = 28 - 2x

3x + 2x = 28 - 33

5x = -5

x = -1

Vậy x = -1.

Bài 2. (2,0 điểm)

a) Ta có: 2a = 5b

frac{a}{5}=frac{b}{2}' width='91' height='41'>(=> frac{a}{5}=frac{b}{2})

Lại có: (frac{a}{5}=frac{3a}{15}; frac{b}{2}= frac{4b}{8})

frac{3a}{15} = frac{4b}{8} = frac{3a+4b}{15+8} = frac{46}{23}=2' width='283' height='42'>(=> frac{3a}{15} = frac{4b}{8} = frac{3a+4b}{15+8} = frac{46}{23}=2)

=> 3a = 2. 15 = 30 => a = 10

4b = 2. 8 = 16 => b = 4.

b) a : b : c = 2 : 4 : 5

frac{a}{2}=frac{b}{4}=frac{c}{5}=frac{a+b-c}{2+4-5}=frac{3}{1}=3' width='312' height='42'>(=> frac{a}{2}=frac{b}{4}=frac{c}{5}=frac{a+b-c}{2+4-5}=frac{3}{1}=3)

=> a = 2. 3 = 6

b = 4. 3 = 12

c = 5. 3 = 15

Bài 3. (1,5 điểm)

Gọi số sách 3 lớp 7A, 7B, 7C quyên góp được là x, y, z (quyển) ((x,y,z in mathbb{N}*))

Vì số sách mà ba lớp 7A,7B,7C quyên góp được tỉ lệ với ba số 5;6;8 nên (frac{x}{5} = frac{y}{6} = frac{z}{8})

Mà số sách lớp 7C quyên góp nhiều hơn số sách của lớp 7A quyên góp là 24 quyển nên z - x = 24

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

(begin{array}{l}frac{x}{5} = frac{y}{6} = frac{z}{8} = frac{{z - x}}{{8 - 5}} = frac{{24}}{3} = 8 Rightarrow x = 5.8 = 40;y = 6.8 = 48;z = 8.8 = 64end{array})

Vậy số sách 3 lớp 7A,7B,7C quyên góp được lần lượt là 40 quyển; 48 quyển và 64 quyển.

Bài 4. (3,0 điểm)

a. Xét tam giác ABM và tam giác MEC có:

BM = MC (M là trung điểm BC)

(widehat{AMB}=widehat{CME})(đối đỉnh)

AM = ME (gt)

=> ΔAMB = ΔMCE (c - g - c)

b. Xét tam giác ABH vuông tại H và tam giác BHD vuông tại H có:

BH là cạnh chung

AH = DH (gt)

=> ΔABH = ΔBDH

=> AB = BD (1)

Ta lại có: ΔAMB = ΔMCE (cmt) => AB = CE (2)

Từ (1) và (2) suy ra CE = BD

c. Từ câu b ta dễ dàng suy ra MA = MD

Vậy tam giác AMD là tam giác cân tại M.

2. Đề thi giữa kì 2 Toán 7 Kết nối tri thức

I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Thay tỉ số 1,25 : 3,45 bằng tỉ số giữa các số nguyên ta được

A. 12,5 : 34,5;

B. 29 : 65;

C. 25 : 69;

D. 1 : 3.

Câu 2. Biết 7x = 4y và y - x = 24. Khi đó, giá trị của x, y là

A. x = −56, y = −32;

B. x = 32, y = 56;

C. x = 56, y = 32;

D. x = 56, y = −32.

Câu 3. Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = -3 thì giá trị của y bằng bao nhiêu?

A. -6;

B. 0;

C. -9;

D. -1.

Câu 4. Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = -12 thì y = 8. Khi x = 3 thì y bằng:

A. -32;

B. 32;

C. -2;

D. 2.

Câu 5. Biểu thức đại số biểu thị “Bình phương của tổng của hai số x và y” là

A. x2 - y2;

B. x + y;

C. x2 + y2;

D. (x + y)2.

Câu 6. Hệ số tự do của đa thức M = 8x2 - 4x + 3 - x5 là

A. 1;

B. 4;

C. 3;

D. 5.

Câu 7. Cho hai đa thức P(x) = 6x3 − 3x2 − 2x + 4 và G(x) = 5x2 − 7x + 9. Giá trị P(x) − G(x) bằng

A. x2 − 9x +13;

B. 6x3 − 8x2 + 5x −5;

C. x3 − 8x2 + 5x −5;

D. 5x3 − 8x2 + 5x +13.

Câu 8.Kết quả của phép nhân (5x − 2)(2x + 1) là đa thức nào trong các đa thức sau?

A. 10x2 − 3x − 2;

B. 10x2 − x + 4;

C. 10x2 + x − 2;

D. 10x2 − x − 2.

Câu 9. Cho tam giác MNP có: (hat{N})=65°; (hat{P})=55°; . Khẳng định nào sau đây là đúng ?

A. MP < MN;

B. MP = MN;

C. MP > MN;

D. Không đủ dữ kiện so sánh.

Câu 10. Cho tam giác MNP có: MN < MP, MD ⊥ NP. Khẳng định nào sau đây là đúng?

A. DN = DP;

B. MD < MP;

C. MD > MN;

D. MN = MP.

Câu 11. Bộ ba độ dài đoạn thẳng nào sau đây không thể tạo thành một tam giác?

A. 15cm; 25cm; 10cm;

B. 5cm; 4cm; 6cm;

C. 15cm; 18cm; 20cm;

D. 11cm; 9cm; 7cm.

Câu 12. Cho ΔABC nhọn có hai đường trung tuyến AM và BN cắt nhau tại O. Khẳng định nào sau đây sai?

A. AO = (frac{2}{3})AM;

B. OM = (frac{1}{3})AM;

C. AO = (frac{2}{3})BN;

D. NO = (frac{1}{3})BN.

II. PHẦN TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm) Tìm x trong các tỉ lệ thức sau:

Bài 2. (1,0 điểm) Ba lớp 7A, 7B, 7C được giao nhiệm vụ trồng 120 cây để phủ xanh đồi trọc. Tính số cây trồng được của mỗi lớp, biết số cây trồng được của ba lớp 7A, 7B, 7C tỉ lệ với 7;8;9.

Bài 3. (2,0 điểm) Cho hai đa thức: P(x) = x3 - 2x2 + x - 2;

Q(x) = 2x3 - 4x2 + 3x - 6.

a) Tính P(x) - Q(x).

b) Chứng tỏ rằng x = 2 là nghiệm của cả hai đa thức P(x) và Q(x).

Bài 4. (2,0 điểm) Cho tam giác ABC có D là trung điểm của AC. Trên đoạn BD lấy điểm E sao cho BE = 2ED. Điểm F thuộc tia đối của tia DE sao BF = 2BE. Gọi K là trung điểm của CF và G là giao điểm của EK và AC. Chứng minh G là trọng tâm tam giác EFC.

Bài 5. (0,5 điểm) Cho tỉ lệ thức (frac{a}{b} = frac{c}{d}). Chứng minh rằng (frac{a−2b}{b} = frac{c - 2d}{d})

Đáp án đề thi giữa kì 2 Toán 7 KNTT

I. Bảng đáp án trắc nghiệm

1.C

2.B

3. A

4.A

5.D

6. C

7.B

8.C

9.C

10.B

11.A

12.C

II. PHẦN TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm) Tìm số hữu tỉ x trong các tỉ lệ thức sau:

Bài 2. (1,0 điểm)

Gọi số cây 3 lớp 7A, 7B, 7C trồng được lần lượt là x, y, z (x,y,z > 0)

Vì tổng số cây trồng của 3 lớp là 120 cây nên x+y+z = 120

Vì số cây trồng được của ba lớp 7A, 7B, 7C tỉ lệ với 7;8;9 nên (dfrac{x}{7} = dfrac{y}{8} = dfrac{z}{9})

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

(begin{array}{l}dfrac{x}{7} = dfrac{y}{8} = dfrac{z}{9} = dfrac{{x + y + z}}{{7 + 8 + 9}} = dfrac{{120}}{{24}} = 5 Rightarrow x = 5.7 = 35y = 5.8 = 40z = 5.9 = 45end{array})

Vậy số cây 3 lớp 7A, 7B, 7C trồng được lần lượt là 35; 40; 45 cây.

Bài 3. (2,0 điểm)

a) Ta có P(x) - Q(x) = (x3 - 2x2 + x - 2) - (2x3 - 4x2 + 3x - 6)

= x3 - 2x2 + x - 2 - 2x3 + 4x2 - 3x + 6

= (x3 - 2x3) + (4x2 - 2x2) + (x - 3x) + (6 - 2)

= - x3- 2x2 - 2x +4.

Vậy P(x) - Q(x) = - x3- 2x2 - 2x +4.

b) Thay x = 2 vào đa thức P(x), ta có:

P(2) = 23 - 2 . 22 + 2 - 2 = 8 - 2 . 4 + 0 = 8 - 8 = 0;

Thay x = 2 vào đa thức Q(x), ta có:

Q(2) = 2 . 23 - 4 . 22 + 3 . 2 - 6 = 2 . 8 - 4 . 4 + 6 - 6

= 16 - 16 + 0 = 0.

Vậy x = 2 là nghiệm của cả hai đa thức P(x) và Q(x).

Bài 4. (1,5 điểm)

Ta có BF = 2BE suy ra BE = EF.

Mà BE = 2ED nên EF = 2ED

Suy ra D là trung điểm của EF

Do đó CD là đường trung tuyến của tam giác EFC.

Vì K là trung điểm của CF nên EK là đường trung tuyến của tam giác EFC.

Tam giác EFC có hai đường trung tuyến CD và EK cắt nhau tại G nên G là trọng tâm của tam giác EFC.

Bài 5 (0,5 điểm)

3. Đề thi giữa kì 2 Toán 7 Cánh diều

I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây.

Câu 1. Thảo ghi chiều cao (cm) của các bạn học sinh tổ 1 lớp 7A được ghi lại trong bảng sau:

130

145

− 150

141

155

151

Số liệu không hợp lí là

A. 155;

B. 141;

C. − 150;

D. 130.

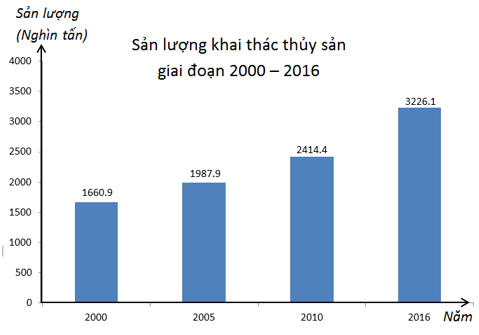
Câu 2. Cho biểu đồ dưới đây

Tiêu chí thống kê là:

A. Giai đoạn 2000 - 2006;

B. Các năm: 2000; 2005; 2010; 2016;

C. Thủy sản;

D. Sản lượng khai thác thủy sản (nghìn tấn).

Câu 3. Biểu đồ đoạn thẳng trong hình dưới đây biểu diễn điểm bài ôn luyện môn Khoa học của bạn Khanh từ tuần 1 đến tuần 5.

Hãy cho biết điểm 7 của bạn Khanh đạt vào tuần nào?

A. Tuần 1 và tuần 2;

B. Tuần 1 và tuần 4;

C. Tuần 2 và tuần 4;

D. Tuần 2 và tuần 5.

Câu 4. Biểu đồ hình quạt tròn biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) chọn loại thực phẩm yêu thích trong 5 loại: Bánh rán, Nước ép, Bánh, Trà, Cà phê của học sinh khối 7 ở trường THCS Thanh Đa. Mỗi học sinh chỉ được chọn một loại thực phẩm khi được hỏi ý kiến như hình bên dưới.

Hỏi tổng số học sinh chọn món Trà và Bánh rán chiếm bao nhiêu phần trăm?

A. 41%;

B. 36%;

C. 64%;

D. 37%.

Câu 5. Khi tung một đồng xu cân đối một lần và quan sát mặt xuất hiện của nó. Số kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu là:

A. 1;

B. 2;

C. 3;

D. 4.

Câu 6. Xác suất của biến cố trong trò chơi có 10 kết quả có thể xảy ra là 2525. Số kết quả thuận lợi của biến cố đó là

A. 5;

B. 2;

C. 4;

D. 6.

Câu 7. Cho ∆ABC vuông tại A. Khi đó

A. (hat{B}) + (hat{C})=90°;

B. (hat{B}) + (hat{C}) =180°;

C. (hat{B}) + (hat{C})=100°;

D. (hat{B}) + (hat{C})==60°.

Câu 8. Cho tam giác ABC. Bất đẳng thức nào dưới đây sai?

A. AB + AC > BC;

B. BC - AB < AC;

C. BC + AB > AC;

D. BC - AC > AB

Câu 9. Cho tam giác MNP có (hat{M}) = 80° và (hat{N}) =50°. So sánh độ dài NP và MP là:

A. NP > MP;

B. NP = MP;

C. NP < MP;

D. Không đủ điều kiện để so sánh.

Câu 10. Cho tam giác ABC và DEH trong hình dưới đây.

Khẳng định đúng là:

A. ∆ABC = ∆DEH;

B. ∆ABC = ∆HDE;

C. ∆ABC = ∆EDH;

D. ∆ABC = ∆HED.

Câu 10. Cho tam giác ABC và tam giác MNP có AB = MP, AC = NM, BC = NP. Khẳng định nào dưới đây đúng?

A. ∆ABC = ∆MNP;

B.∆ABC = ∆NMP;

C.∆ABC = ∆PMN;

D.∆ABC = ∆MPN.

Câu 11. Phát biểu đúng là

A. Nếu hai cạnh và góc xen giữa của tam giác này lần lượt bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau;

B. Nếu hai cạnh và một góc của tam giác này bằng hai cạnh và một góc của tam giác kia thì hai tam giác đó bằng nhau;

C. Nếu hai cạnh của tam giác này bằng hai cạnh của tam giác kia thì hai tam giác đó bằng nhau;

D. Nếu một góc của tam giác này bằng một góc của tam giác kia thì hai tam giác đó bằng nhau.

Câu 12. Cho tam giác ABC có M là trung điểm cạnh BC. Kẻ tia Ax đi qua M. Qua B, C lần lượt kẻ các đường thẳng vuông góc với Ax, cắt Ax tại H và K. So sánh BH và CK.

A. BH < CK;

B. BH = 2CK;

C. BH > CK;

D. BH = CK.

II. PHẦN TỰ LUẬN (7,0 điểm)

Bài 1. (2,0 điểm) Xét tính hợp lí của các dữ liệu trong mỗi bảng thống kê sau:

a)

Lớp

Sĩ số

Số học sinh tham gia ngoại khóa

7A1

39

42

7A2

42

10

7A3

45

15

7A4

43

26

Tổng

169

60

b)

Kết quả kiểm tra thường xuyên môn Toán đợt 1

Tỉ lệ phần trăm

Từ 8 điểm trở lên

45%

Từ 6,5 điểm đến 7,9 điểm

110%

Từ 5,0 điểm đến 6,4 điểm

35%

Từ 3,5 điểm đến 4,9 điểm

10%

Dưới 3,5 điểm

200%

Bài 2. (1,0 điểm) Một hộp có 48 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; …; 48. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số chính phương”.

Bài 3. (3,0 điểm)

Cho tam giác ABC vuông tại A, (widehat{B}={{60}^{0}}), AB = 5cm. Tia phân giác góc B cắt AC tại D. Từ D kẻ đường thẳng vuông góc với BC tại E.

a. Chứng minh rằng (Delta ADB=Delta BDE)

b. Chứng minh tam giác AEB là tam giác đều.

c. Tính BC.

Bài 4. (1,0 điểm) Năm 2020, Việt Nam xuất khẩu (ước đạt) 6,5 triệu tấn gạo, thu được 3,07 tỉ đô la Mỹ. Biểu đồ hình quạt tròn ở bên dưới biểu diễn khối lượng xuất khẩu của mỗi loại gạo trong tổng số gạo xuất khẩu (tính theo tỉ số phần trăm).

Dựa vào thông tin thu thập từ biểu đồ trên để trả lời các câu hỏi sau:

a) Tính số lượng gạo trắng và số lượng gạo nếp được xuất khẩu năm 2020?

b) Số lượng gạo trắng xuất khẩu nhiều hơn số lượng gạo thơm là bao nhiêu?

Đáp án Đề kiểm tra giữa kì 2 Toán 7 Cánh diều

PHẦN TRẮC NGHIỆM

1. C2. D3. B4. A5. B6. C7. A8. D9. A10. D11. A12. D

PHẦN TỰ LUẬN (7,0 điểm)

Bài 1. (2,0 điểm)

a) Bảng thống kê này chưa hợp lí:

Số học sinh lớp 7A1 tham gia ngoại khoá (42 học sinh) vượt quá sĩ số của lớp (39 học sinh);

Tổng số học sinh tham gia ngoại khoá của các lớp là:

42 + 10 + 15 + 26 = 93 (học sinh).

Tổng số học sinh tham gia ngoại khoá của các lớp (93 học sinh) lớn hơn số học sinh ở phần tổng (60 học sinh) nên bảng thống kê này chưa hợp lí.

b) Bảng thống kê này chưa hợp lí vì tỉ lệ phần trăm kết quả kiểm tra thường xuyên không thể vượt quá 100% (cột tỉ lệ phần trăm kiểm tra thường xuyên môn Toán đợt 1 dưới 3,5 điểm là 200% vượt quá 100%) và tổng các loại phải đúng bằng 100%.

Bài 2. (1,0 điểm)

Tập hợp các kết quả có thể xảy ra là: {1; 2; 3; … ; 47; 48}. Có 48 kết quả.

Trong các số trên, số chính phương là: 1; 4; 9; 16; 25; 36.

Do đó có 6 kết quả thuận lợi.

Khi đó, xác suất của biến cố đã cho là: 6 48 = 1 8 648=18 .

Vậy xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số chính phương” bằng 1 8 18 .

Bài 3. (3,0 điểm)

a. Xét tam giác ABD vuông tại A và tam giác BDE vuông tại E có:

BD cạnh chung

(widehat{ABD}=widehat{DBE}={{30}^{0}})(BD là phân giác góc B)

(Rightarrow Delta ADB=Delta BDE)(cạnh huyền - góc nhọn)

b. Ta có: (Delta ADB=Delta BDERightarrow AB=BE)

Xét tam giác ABE có AB = BE, (widehat{B}={{60}^{0}})

Vậy tam giác ABE là tam giác đều.

c. Ta có tam giác ABE là tam giác đều

=> AB = BE = AE = 5cm (*)

(Rightarrow widehat{BAE}=widehat{ABE}={{60}^{0}})

Mặt khác (widehat{BAC}={{90}^{0}})

(Rightarrow widehat{EAC}=widehat{BAC}-widehat{BAE}={{90}^{0}}-{{60}^{0}}={{30}^{0}}) (1)

Xét tam giác ABC có:

(begin{align} & widehat{ABC}+widehat{BCA}+widehat{BAC}={{180}^{0}} & Rightarrow widehat{BCA}={{180}^{0}}-widehat{ABC}-widehat{BAC} & Rightarrow widehat{BCA}={{180}^{0}}-{{60}^{0}}-{{90}^{0}} & Rightarrow widehat{BCA}={{30}^{0}}text{ }left( 2 right) end{align})

Từ (1) và (2) ta có tam giác AEC cân tại E

=> AC = EC = 5cm (**)

Từ (*) và (**) suy ra BC = BE + EC = 5 + 5 = 10cm

Bài 4. (1,0 điểm)

a) Số lượng gạo trắng được xuất khẩu năm 2020là:

6,5 . 45,2% = 2,938 (triệu tấn).

Số lượng gạo nếp được xuất khẩu năm 2020là:

6,5 . 9% = 0,585 (triệu tấn).

Vậy số lượng gạo trắng và số lượng gạo nếp được xuất khẩu năm 2020 lần lượt là 2,938 triệu tấn và 0,585 triệu tấn.

b) Số lượng gạo thơm được xuất khẩu là:

6,5 . 26,8% = 1,742 (triệu tấn).

Tỉ số phần trăm số lượng gạo trắng xuất khẩu nhiều hơn số lượng gạo thơm là:

2,938 - 1,742 = 1,196 (triệu tấn).

Vậy số lượng gạo trắng xuất khẩu nhiều hơn số lượng gạo thơm 1,196 triệu tấn.

...........................

Kỳ thi giữa học kì 2 lớp 7 năm 2023 - 2024 sắp diễn ra, để chuẩn bị cho kì thi sắp tới đạt kết quả cao, VnDoc gửi tới các bạn chuyên mục Đề thi giữa kì 2 lớp 7 với đầy đủ các môn, do VnDoc biên soạn hoặc sưu tầm từ nhiều trường THCS trên cả nước. Đây là bộ tài liệu phong phú, hữu ích cho các thầy cô tham khảo ra đề, cũng như các em học sinh ôn luyện, làm quen với nhiều dạng đề khác nhau, chuẩn bị cho kì thi sắp tới đạt kết quả cao. Chúc các em học tốt.

Đề thi giữa kì 2 lớp 7 môn khác

Link nội dung: https://appstore.edu.vn/de-toan-7-giua-ki-2-a65874.html