Góc đối đỉnh là gì? Liệu hai góc đối đỉnh có giống nhau không?

1. Khái niệm về góc đối đỉnh

Góc đối đỉnh là hai góc có cạnh của góc này là tia đối diện với một cạnh của góc kia.

Khi hai đường thẳng a và b cắt nhau, chúng tạo thành các cặp góc đối đỉnh như minh họa trong hình vẽ.

Còn có một cặp góc đối đỉnh khác:

Khi hai đường thẳng cắt nhau, chúng tạo ra hai cặp góc đối đỉnh.

Ví dụ 1: Hai góc này có phải là góc đối đỉnh không?

Giải thích:

Để xác định hai góc có phải là góc đối đỉnh hay không, ta dựa vào định nghĩa rằng 'mỗi cạnh của góc này là tia đối của một cạnh góc kia.'

Từ hình vẽ, ta thấy rằng tia Ot không phải là tia đối của tia Õ.

Vì vậy, hai góc này không phải là góc đối đỉnh.

Ví dụ 2: Liệu hai góc này có phải là góc đối đỉnh không?

Giải thích:

Dựa vào định nghĩa rằng 'mỗi cạnh của góc này là tia đối của một cạnh góc kia'

Chọn bất kỳ cạnh nào trong hai góc, ta thấy rằng nó không phải là tia đối của bất kỳ cạnh nào ở góc kia.

Do đó, hai góc này không phải là góc đối đỉnh.

2. Đặc điểm của hai góc đối đỉnh

- Hai góc đối đỉnh luôn bằng nhau

Chứng minh:

Chúng ta sẽ chứng minh rằng góc O1 và góc O3 là bằng nhau.

Vì góc O1 và góc O2 là kề bù, nên tổng của chúng là 180° (1).

Vì góc O3 và góc O2 cũng là kề bù, nên tổng của chúng là 180° (2).

Từ (1) và (2), ta suy ra rằng góc O1 + góc O2 = góc O3 + góc O2

Do đó, góc O1 bằng góc O3.

Cặp góc đối đỉnh O2 và O4 cũng được chứng minh tương tự.

Ví dụ 3: Hai đường thẳng cắt nhau tạo ra các góc như trong hình. Biết rằng số đo của góc ba là 40°. Hãy tìm số đo của các góc còn lại.

Giải thích:

Khi hai đường thẳng cắt nhau, chúng tạo thành các góc 1, 2, 3 và 4. Do đó, góc 1 và góc 3 là hai góc đối đỉnh.

Vì vậy: góc O1 = góc O3 = 40°

Góc O2 và góc O3 là hai góc kề bù, nên tổng của chúng là 180°: góc O3 + góc O2 = 180°

Vì góc O3 = 40°

Do đó, góc O2 = 180° - 40° = 140°

Góc O2 và góc O4 là hai góc đối đỉnh, vì vậy góc O4 = góc O2 = 140°

Do đó, số đo của các góc O1, O2, O3, O4 lần lượt là 40°, 140°, 40°, 140°

Ví dụ 4: Biết rằng hai góc dưới đây là đối đỉnh. Tìm giá trị của x.

Giải thích:

Vì hai góc trên là góc đối đỉnh, nên chúng có giá trị bằng nhau.

Vì vậy ta có:

2x + 50 = 3x

Kết luận x = 50

* Lưu ý: Hai góc bằng nhau chưa hẳn là góc đối đỉnh.

3. Các dạng bài tập cơ bản

3.1. Dạng 1: Hoàn thiện câu phát biểu hoặc chọn câu trả lời chính xác

1. Phương pháp giải quyết

- Tham khảo các kiến thức lý thuyết tương ứng trong sách giáo khoa để điền đúng chỗ trống hoặc chọn câu phát biểu chính xác.

- Sử dụng hình vẽ để bác bỏ các câu sai.

2. Ví dụ minh họa:

Ví dụ 1: Hoàn thành các câu sau đây:

a, Hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia được gọi là hai góc ...........

b, Khi hai đường thẳng cắt nhau, chúng tạo thành ................................................................................................

Giải đáp:

a, Hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia được gọi là hai góc đối đỉnh.

b, Khi hai đường thẳng cắt nhau, chúng tạo thành hai cặp góc đối đỉnh.

3.2. Dạng 2: Vẽ hình theo yêu cầu trong đề bài và xác định các cặp góc đối đỉnh hoặc không phải đối đỉnh.

1. Phương pháp giải:

- Sử dụng thước thẳng, eke và thước đo góc để vẽ hình chính xác.

- Xem xét các cạnh của góc và các tia đối để xác định các cặp góc đối đỉnh.

2. Ví dụ minh họa

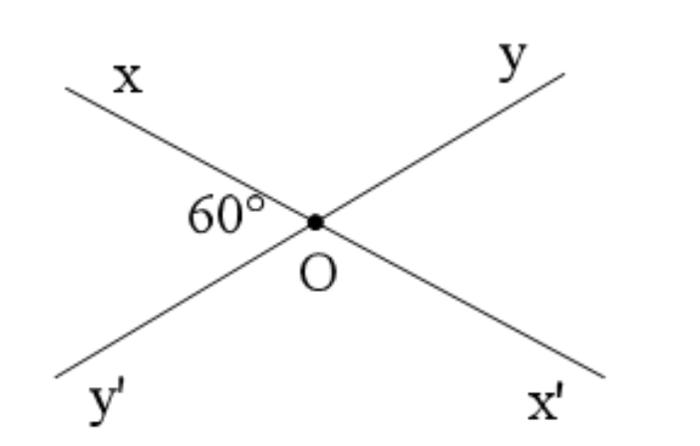
Ví dụ 2: Hai đường thẳng xx' và yy' cắt nhau tại điểm O, tạo ra bốn góc, trong đó có một góc có số đo là 60°. Hãy liệt kê các cặp góc đối đỉnh.

Cặp góc đối đỉnh đầu tiên là góc xOy' và góc x'Oy vì Ox và Ox'; Oy và Oy' là các tia đối nhau.

Cặp góc đối đỉnh thứ hai bao gồm góc xOy và góc x'Oy', vì Ox và Ox'; Oy và Oy' là các tia đối nhau.

3.3. Dạng 3: Vẽ hình và tính toán số đo của các góc

1. Phương pháp giải:

- Vẽ hình theo đúng yêu cầu của đề bài.

- Áp dụng các tính chất liên quan:

• Hai góc bù nhau có tổng bằng 180°
• Hai góc kề bù cũng có tổng bằng 180° vì chúng bù nhau.
• Hai góc đối đỉnh luôn bằng nhau.

2. Ví dụ minh họa

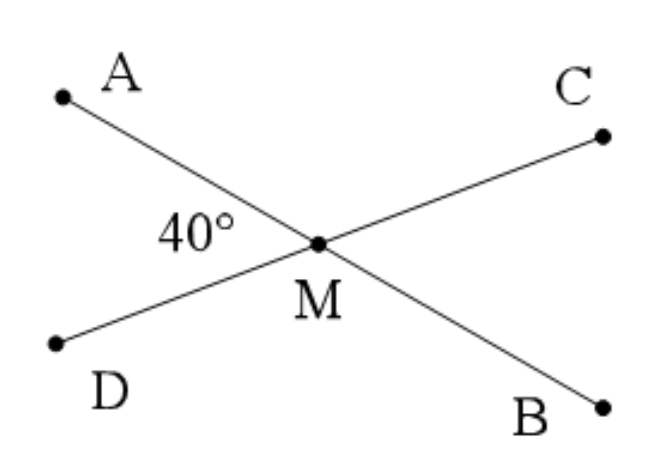
Ví dụ 3: Hai đường thẳng AB và CD cắt nhau tại điểm M. Biết rằng góc AMD có số đo là 40°. Tính số đo của các góc BMC và BMD.

Vì góc AMD và góc BMC là hai góc đối đỉnh nên góc AMD = góc BMC = 40°

Góc AMD và góc BMD là hai góc kề bù, nên tổng của chúng là 180°.

Do đó, góc BMD = 180° - góc AMD = 180° - 40° = 140°

Vậy góc BMC = 40° và góc BMD = 140°

3.4. Dạng 4: Xác định các cặp góc bằng nhau

1. Phương pháp giải: Áp dụng tính chất rằng hai góc đối đỉnh thì bằng nhau.

2. Ví dụ minh họa

Ví dụ 4: Ba đường thẳng AB, CD, EF cắt nhau tại điểm O như trong hình. Xác định các cặp góc nhỏ hơn góc bẹt và bằng nhau trên hình.

Giải đáp:

Trên hình, ba đường thẳng AB, CD và EF đều cắt nhau tại điểm O.

Các cặp góc nhỏ hơn góc bẹt và bằng nhau trên hình gồm:

Góc AOC bằng góc BOD

Góc EOC bằng góc DOF

Góc BOE bằng góc AOF

Góc AOE bằng góc BOF

Góc BOC bằng góc AOD

Góc DOE bằng góc COF

. Dạng 5: Xác định các tia đối nhau

1. Phương pháp giải

Áp dụng kiến thức: Nếu hai góc kề nhau có tổng bằng 180°, thì hai cạnh ngoài của chúng là các tia đối nhau.

2. Ví dụ minh họa

Ví dụ 5: Hai đường thẳng AB và CD cắt nhau tại điểm O. OM và ON lần lượt là tia phân giác của góc AOC và góc BOD. Giải thích tại sao OM và ON là hai tia đối nhau?

Góc AOC cộng với góc COB tạo thành góc AOB, mà góc AOB bằng 180° (vì là hai góc kề bù) (1)

Vì OM và ON là tia phân giác của góc AOC và góc BOD, đồng thời góc AOC bằng góc BOD (hai góc đối đỉnh)

Góc AOM bằng góc COM, góc BON, góc DON, góc AOC chia đôi và cũng bằng góc BOD chia đôi.

Từ đó, góc COM cộng với góc BON sẽ bằng góc AOC chia đôi cộng góc AOC chia đôi, tức là bằng góc AOC.

Kết hợp hai thông tin trên, ta có góc COM cộng góc BOC cộng góc BON bằng 180°.

Do đó, góc MON bằng 180°.

Chúng ta thấy hai tia OM và ON tạo với nhau một góc 180° tại đỉnh O.

Do đó, OM và ON là hai tia đối xứng.

4. Bài tập ứng dụng

Câu 1: Chọn câu đúng: Hai góc đối đỉnh là:

A. hai góc bằng nhau

B. hai góc có cùng đỉnh

C. hai góc mà mỗi cạnh của chúng là tia đối của một cạnh của góc kia

D. hai góc nằm trên hai nửa mặt phẳng khác nhau

Câu 2: Mối quan hệ của số đo hai góc đối đỉnh được tạo ra bởi hai đường thẳng cắt nhau là gì?

A. Tổng số đo của hai góc đối đỉnh là 360°

B. Tổng số đo của hai góc đối đỉnh là 180°

C. Hiệu của số đo hai góc đối đỉnh bằng 0°

D. Tổng của số đo hai góc nhọn đối đỉnh là 180°

Câu 3: Vẽ theo chỉ dẫn sau: Trên đường thẳng aa', chọn điểm O. Vẽ tia Ot sao cho góc aOt là góc tù. Trên nửa mặt phẳng đối diện với tia Ot, vẽ tia Ot' sao cho góc a'Ot' là góc nhọn.

Dựa vào hình vẽ, hãy xác định xem góc aOt và góc a'Ot' có phải là cặp góc đối đỉnh không? Giải thích vì sao?

Bài viết của Mytour về định nghĩa và tính chất của hai góc đối đỉnh. Hy vọng thông tin trong bài viết sẽ hữu ích cho bạn đọc. Cảm ơn bạn đã theo dõi!